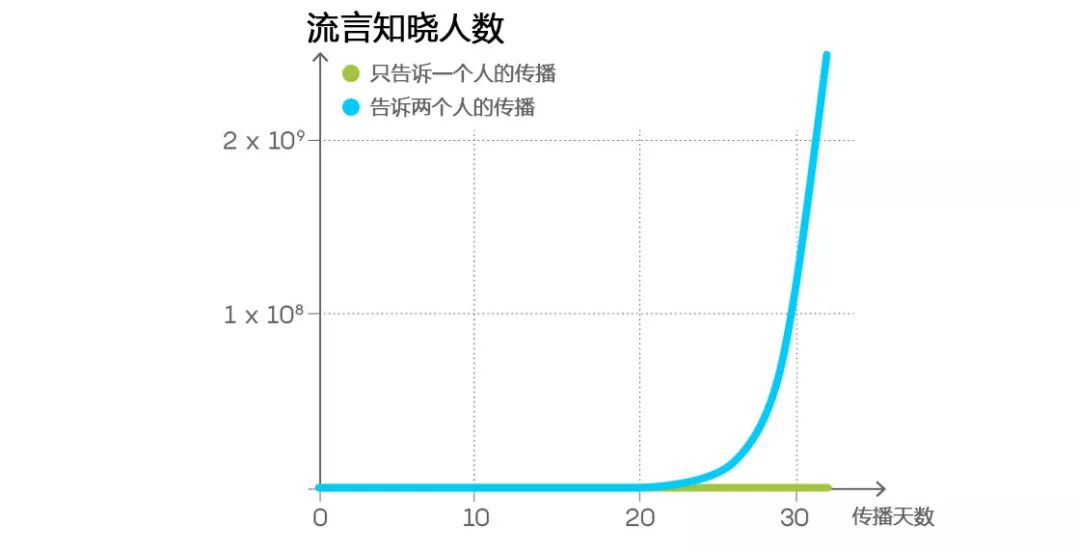
我们假设你听到了一个添油加醋的谣言,你没忍住告诉了别人。好在大家都不喜欢当八婆,都只告诉一个人,然后就不再和其他人再提起这件事。这就没什么大不了的,是吧?毕竟,如果每个人都遵照这个传播规则——只告诉一个人,然后闭嘴——那么这个留言不会传播得太快太远。假设每天有1个人听到这件事,30天后,也只有31个人知道它,这31个人当中,还包括你自己。
但是,如果每个人给两个人说这件事呢,事情会怎么样呢?那会变得相当的恐怖!如果每天,每个人向2个之前不知道的人传播谣言,那么30天后,超过全球四分之一的人会知道它(2 ^31 -1 = 2,147,483,647 的人,2^31表示2的31次方)。我们不过就是把之前的告诉一个人变成告诉两个人而已,为什么这一个小小的变化会导致结果巨大的改变?答案就在两者增长方式的变化率上。
第一个场景中,听到谣言的人数是以相同数量新增的,都和昨天一样。今天新增多少,明天新增多少,后天新增多少,统统一样。就是说,每天新增的谣言知晓人数是固定不变的常数。在我们给的例子中,这个常数等于1 。
但是,如果听到流言的新增人数都两倍于昨天,那么新增人数就是指数增长:第一天2个人听到谣言。第二天,就会新增4个谣言知晓新增人数,第三天就8个,一直持续。到第30天的时候,就有2^30(2的30次方)的人第一次听到流言。
为什么两个场景的产生的结果有如此之大的差异?这个和线性函数与指数函数的性质有关。线性函数的增长率是一个常数,比如第一个场景里,每天新增的谣言知晓人数。线性函数,增长是缓慢而稳定的。在相同时间内,增长的数量是恒定的。指数函数是另外一种增长模式,它是按照某种比例成倍增长:2个人知道了流言,然后告诉4个人、8个人、16个人……,和线性函数的增长不一样,指数函数的增长是不断加速的增长——增长量本身还在持续增长。
这就是造成30天后,一个结果是31,另一个结果是20亿,如此巨大差别的原因。就是说,当你听到谣言时,你扩散给一个人还是两个人,就有如此之大的差别。
这里有个简易的数学模型,来揭示那些具有复制传播特征现象的本质,他能解释的东西远远不止谣言传播那么狭窄。当然,和所有的简易模型一样,为了简化,暂不考虑一些复杂的因素——比如传播概率和传播载体总量——但这个模型依然能解释清楚类似疾病、谣言是如何越传越多,越传越大的。
疾病的传染和谣言的传播有很大的相似之处:从某个人发起,然后传播到另外的人。两者当然有区别,但是这个简易的数学模型是适合这两种不同情况的。在刚刚关于谣言的简单示例中,我们看到了看似很小的谣言传播速度差异如何造成最终人数数量差异。在传染病方面也是如此,疾病能传染给一个人与能传染给两个人之间的差异,可能就是一些普通传染病与流行病之间的差异。
每一种传染病都在某个范围内传播,其传播速度取决于疾病的生物特性、环境因素、社会因素。流行病学家试图总结所有这些因素对感染的“基本再生数”(basic reproduction number)的影响。这是每个感染者预期传播给新的感染者的平均数量,用R0表示。在上面我们的谣言传播的两个不同例子中,基本再生数分别是R0 = 1(每个人只将谣言传播给一个人)和R0 = 2(每个人将谣言传播给两个人); “传染期”是一天。
下面是一些常见疾病的基本再生数(数据引自美国CDC和NIH)。
麻疹:12≤R0≤18
天花:5≤R0≤7
腮腺炎:4≤R0≤7
1918流感:2≤R0≤3(哆嗒数学网小编注:1918年流感让超过千万人失去生命)
注意,所有的基本再生数都是大于1 。这就是这些疾病为什么那么危险的原因:由于每个感染者平均感染的人数都超过1,因此感染这种疾病的人数将成为指数增长。这可能对我们人类造成毁灭性影响。那么,这个已知被基本再生数标定指数增长的是否可以被降低成线性线增长?我们是否有办法把R0降低成为1呢?
接种疫苗就产生了这种效果。接种疫苗后,一个人会产生对该疾病的抵抗力,但成功率不尽相同。但为简单起见,我们将假定疫苗接种可完全抵抗该疾病。疫苗接种不仅直接使接种疫苗的个体受益,也间接使其他广大人群受益。如果传播范围内有很多人接种了某种疾病的疫苗,这种疾病的传播速度将不会很快。
实际上,广泛的疫苗接种可以帮助减少疾病的有效再生数。而且,如果有足够多的人接种疫苗,那么有有效再生数实际上可以降到1,从而确保该疾病只会以线性速度传播。那么,需要多少人进行疫苗接种才能使疾病的有效再生数减少到1呢?
我们来看看基本再生数揭示的真正含义。考虑一种流感的R0=2,就是说,一个感染者平均会传染2个新的感染者。这个R0=2这个数字,其实告诉了我们很多信息:传播难易程度、感染周期、一定时期内感染者的接触人数。通过理解这个数字,我们能容易理解疫苗接种是如何降低流行病爆发风险的。
我们假设有个人感染了一种流感病毒,而这个人会接触10个人,并假设这个传染病的的R0等于2。我们可以画个图,被感染者用绿色表示,而连线的方向指向每一个他接触的人。

每一个接触者都是有一定几率被传染上的,但由于我们假设R0=2,也就是假设平均意义上说,有2个人会染上这个病。
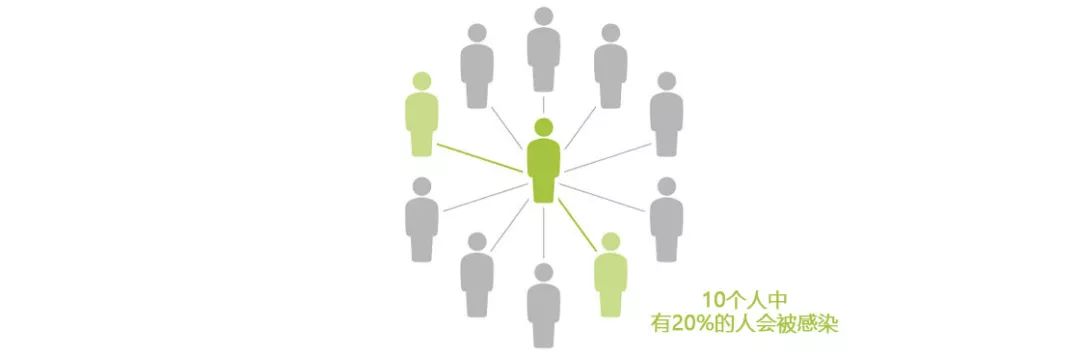
现在,我们再假设10个人中有2个人接种了该流感的疫苗。所以,我们再简化一下,认为接种后的人是完全免疫者,就是说这些人不可能患得此病。但剩下的8个人仍然有20%的可能性感染,就是说,平均意义上看有,10个人中有0.2×8 =1.6个人会被感染。
所以,如果每个人的10个接触者中有2人接种了疫苗,被感染的人在平均意义上只会传染1.6个人。接种疫苗有效使得该病的基本再生数从2降到了1.6。那么我们进一步怎么做,可以让增长方式不再是指数增长呢?
再来,我们假设初期的感染者在传染期内都接触10个人,每个没有接种疫苗的人有20%的几率感染病毒。现在,假设10个人中有V个人接种了疫苗。我们可以计算,平均意义上,10-V个人中有20%的人会被感染,也就是0.2×(10-V)的人会被感染。为了使得增长变为线性的而不是指数的,那么平均感染人数需要是1。因此,我们需要解方程:0.2×(10-V)=1。
用一点点代数知识解得V=5。所以,我们来看如果10接触者中,有5个人接种了疫苗会发生什么。我们把接种疫苗的人涂成蓝色。
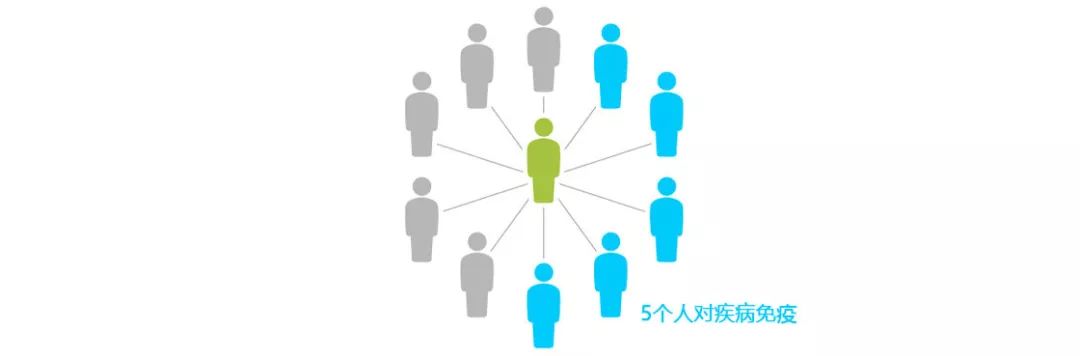
被接种者实际上在图中被剔除了,因为按假设他们不会被病毒侵染。
现在剩下的5个人依然有20%的可能性感染,所以平均有1个人感染了病毒。这就是说,原来患者接触的10个人,最后只有1个人被传染。所以,由于10个人中有5个人接种了疫苗,我们有效的把R0降低成为了1。

这个过程可以推广成对任意基本再生数R0的计算。我们假设每个感染者在传染期内接触N个人,我们可以计算,平均上这N个人中有R0/N比例人会被传染。但是,如果N个人中有V个人接种了疫苗,那么下面的式子就表示平均有多少人会被一个人传染:
(N-V)R0/N
(N-V)R0/N = 1
V/N表示,总体人口中,有多少比例的人接种了疫苗。我再整理一下式子,抽象的解出V/N:
V/N = 1 – 1/R0
就是说,如果总体中有1-1/R0比例的人口接种了疫苗,那么平均意义上,每个人只能传染1个人。因此,1-1/R0奇迹般的让传染病的扩散增长方式变成了线性,而不再是指数。
在这种疫苗接种水平下——总体中有1-1/R0比例人接种疫苗——整个总群都获得对某种疾病的免疫能力:不止是接种疫苗的免疫个体可以免于疾病,而且整个种群中疾病传染速度也免于指数增长。这个现象就叫做“群体免疫”(herd immunity)。接种率需要达到多少,就能得到群体免疫效果的那个比例,叫做“群体免疫阈值”(herd immunity threshold, HIT)。
麻疹:R0=12,HIT = 1 – 1/12 = 91.7%
天花:R0=5,HIT = 1 – 1/5 = 80%
腮腺炎:R0=4,HIT = 1 – 1/4 = 75%
1918流感:R0=2,HIT = 1 – 1/2 = 50%
显然,接种疫苗对抗疾病的意义并不单单是对每一个个体有好处,同样对整个社会有大大的好处。当免疫个体达到临界点数量,疾病的传播率会维持一个足够低的水平,从而让整个种群避免灾难性后果。接种疫苗让疾病的传播方式本来可能是下图左边的方式变成右边的方式,当很多潜在的传染路径像图中右边的方式被斩断,那么传染速度就会被降低,从而降低流行病大爆发的可能性。
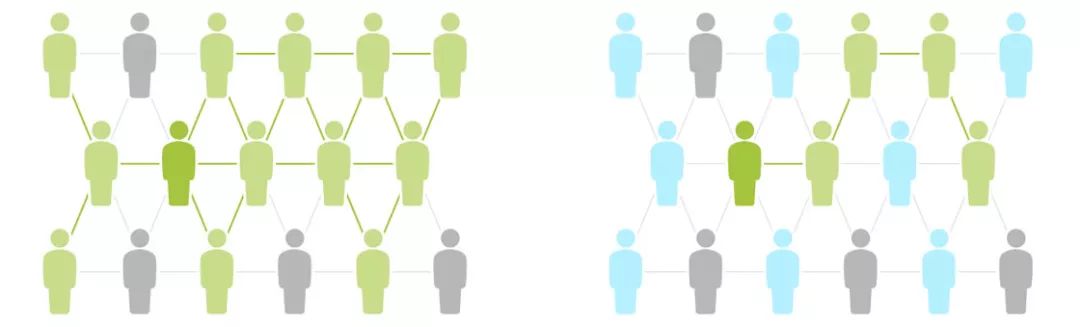
一个关于群体免疫的重要特征是, 哪怕没有接种疫苗的个体也从中获益。因为传染病被降低了更广泛传播的可能性,每个的感染概率都降低了——没有接种疫苗的人也是如此。这一点,对那些在医学上不适合接种疫苗的人特别重要,比如婴儿、老人以及其他体弱者。虽然,我们的假设是疫苗100%有效,但达成种群免疫的效果并不需要疫苗100%有效:就算不能100%有效,疫苗仍然能降低每个感染者传染人数的平均数量,从而降低传染病的有效再生数。(这里接种疫苗只是避免被感染的手段之一,这几段其实在数学上说明了个体不被感染其实也是对整个社会的贡献。——哆嗒数学网小编注)。
我们看到了线性增长和指数增长的夸张差别。当传染病开始流行,那就是关乎生死的大事情。这里用数学描述的对个人的避免感染和对社会的达到群体免疫都是非常重要的点。你可以讲给周围的人听。











